数据结构与算法-01-绪论

发表于 2022-10-26 更新于 2022-10-28 分类于数据结构阅读次数：本文字数： 3.2k 阅读时长 ≈ 3 分钟

第一章绪论

数据结构起源

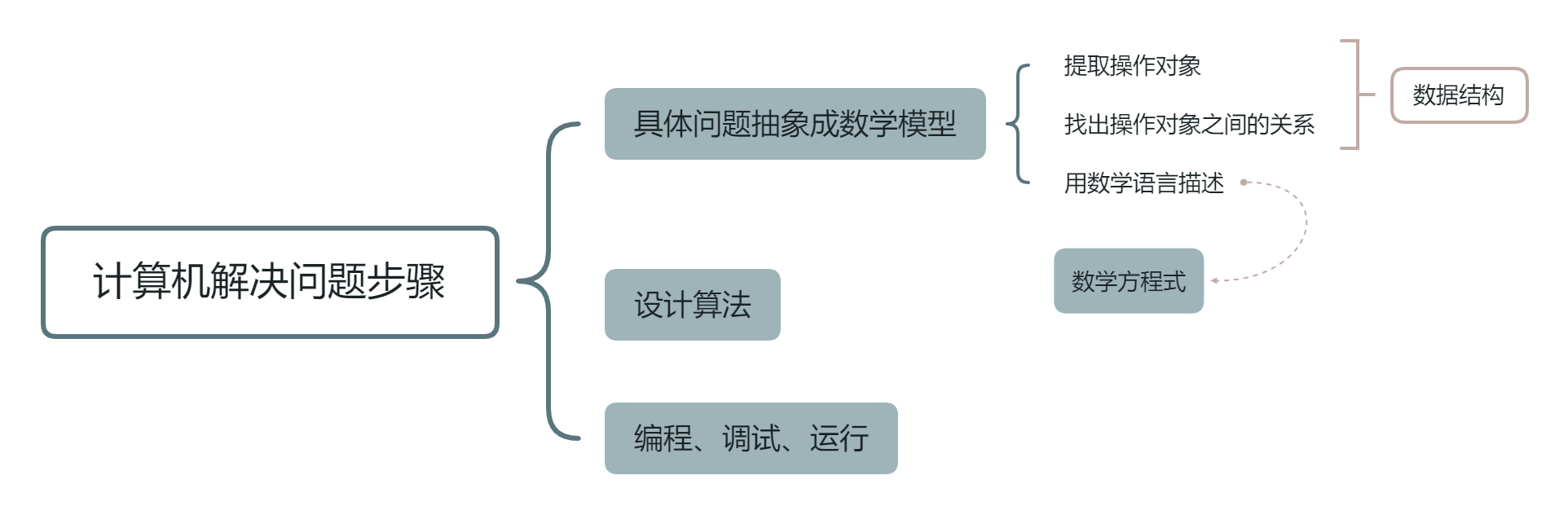
数据结构：操作对象和操作对象之间的关系

操作对象为数值对象
- 举例：
  
  数学模型：KU=M 线性方程组 \[ \left[\begin {array}{c} a_{11}\ a_{12}\ a_{13}\\ a_{21}\ a_{22}\ a_{23}\\ a_{31}\ a_{32}\ a_{33}\\ \end{array}\right] \times \left[\begin {array}{c} x_{1}\\ x_{2}\\ x_{3}\\ \end{array}\right] = \left[\begin {array}{c} b_{1}\\ b_{2}\\ b_{3}\\ \end{array}\right] \]
  - 操作对象：K、U、M
  - 对象关系：KU=M
  - 特点：数据元素间的关系简单，计算复杂，因此研究的重点是计算方法（如数值分析里的高斯消去法等）
- 数值型的算法指的是解法，而非数值型指的是操作的步骤

计算机应用于非数值的计算

举例1

学号	姓名	性别	籍贯	专业
60214201	杨阳	男	安徽	计算机科学与技术
60214202	薛林	男	福建	计算机科学与技术
60214215	王诗萌	女	吉林	计算机科学与技术
60214216	冯子晗	女	山东	计算机科学与技术

操作对象：每位学生的信息（包含姓名、性别、籍贯、专业）
对象关系：线性关系（一个接一个）－> 数据结构：线性表
涉及算法：增删改查

举例2

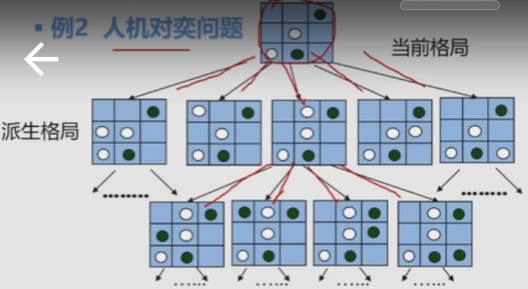
井字棋人机对弈问题
- 操作对象：棋局（棋盘的格局信息）
- 对象关系：非线性关系（1：n）－> 数据结构：树
- 涉及算法：走棋（选择一种策略使棋局发生变化）

总结：
1. 从性质上看，两个例子（表与树）的共性是均无法用数学数学公式或方程来描述，隶属于非数值的程序设计问题
2. 从关系上看，描述非数值计算问题的数学模型不是数学方程，而是类似表、树、图等具有逻辑关系的数据
3. 综上，数据结构是一门研究非数值计算的程序设计中的计算机的操作对象以及它们之间关系和操作的学科

数据结构概念

基本概念

数据：输入计算机且能被计算机处理的各种符号的集合，包含数值型（整数、实数等）和非数值型（文字、图像、声音等）两类
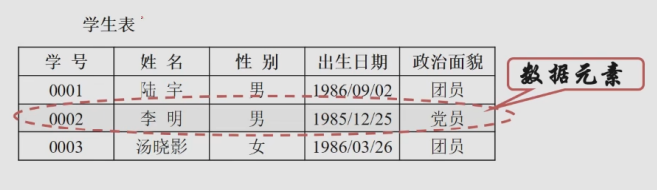
数据元素：（记录、结点或顶点）数据的基本单位，在计算机程序中通常作为一个整体进行考虑和处理
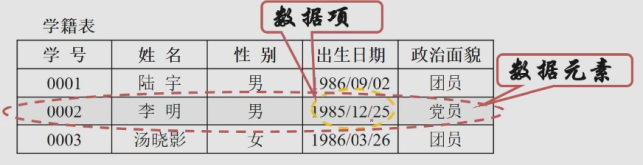
数据项：构成数据元素的不可分割的最小单位
- 数据 > 数据元素 > 数据项。
- 数据表 > 个人记录 > 学号、姓名等
数据对象：性质相同的数据元素的集合，是数据的一个子集
数据结构：相互之间存在一种或多种特定关系的数据元素的集合
1. 逻辑结构
  - 描述数据元素之间的逻辑关系
  - 与数据的存储无关、独立于计算机
  - 是从具体问题抽象出来的数学模型
2. 物理结构（存储结构）
  - 数据元素及关系在计算机存储器中的结构（存储方式）
  - 是数据结构在计算机中的表示
3. 逻辑结构与存储结构的关系
  - 存储结构是逻辑关系的抽象与元素本身的映像
  - 逻辑结构是数据结构的抽象，存储结构是数据结构的实现
  - 两者综合起来建立了数据元素之间的结构关系

逻辑结构的分类

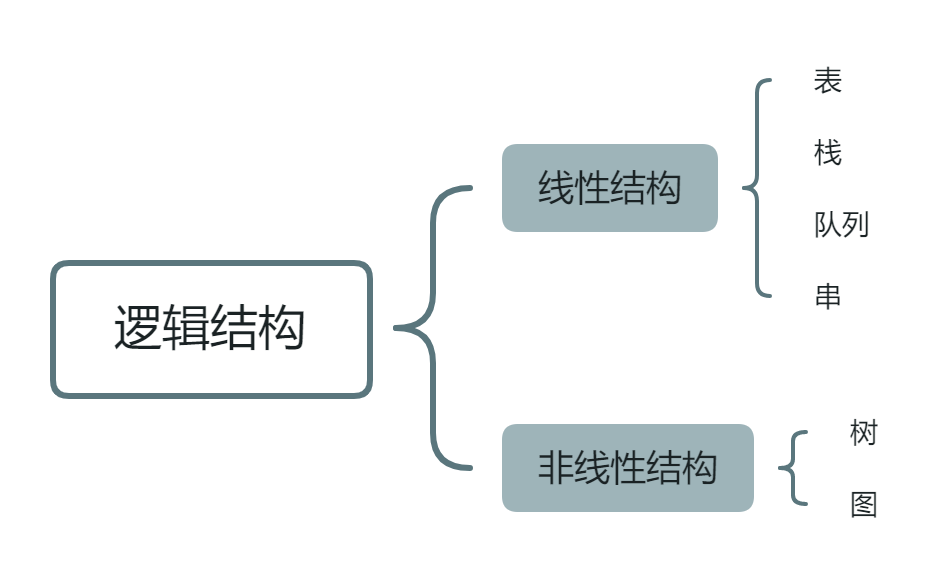
逻辑结构
- 线性结构
  - 仅有一个开始和终端结点
  - 所有结点最多只有1个直接前趋和1个直接后继（1：1）
- 非线性结构
  - 一个结点可能有多个直接前趋和直接后继（1：n/m：n）
- 集合结构：无关系，仅属于一个集合
- 线性结构：数据元素1：1线性关系
- 树形结构：1:n
- 图/网状结构：m:n
物理结构（存储结构）
- 连续的存储单元依次按位置存储数据元素
- C语言用数组实现顺序存储结构
- 任意存储单元存储
- C语言用指针实现链式存储结构

数据类型和抽象数据类型

数据类型：性质相同的值的集合以及定义域这个值集合上的一组操作的总称（明显或隐含地规定变量的取值范围以及范围上允许的操作）

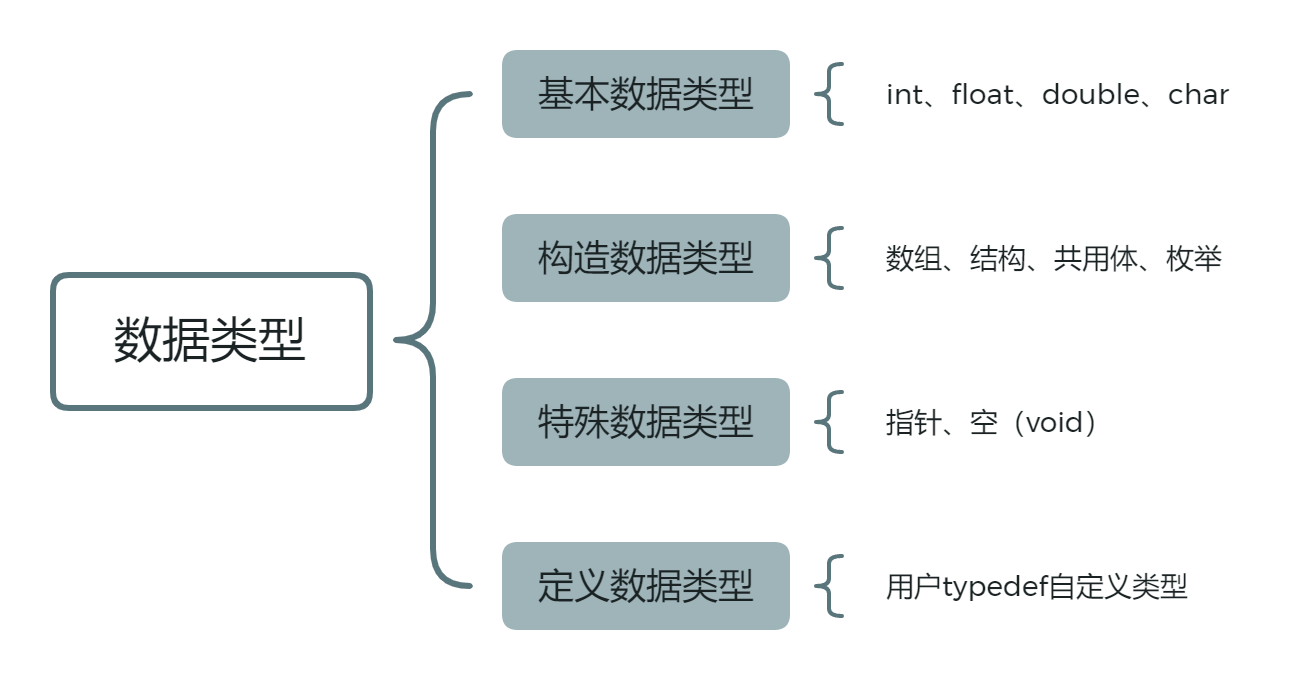
注意：

基本数据结构可以用数据类型实现，如数组、字符串等

其它常用数据结构如栈、队列、树、图等不能直接用数据类型表示

抽象数据类型：指一个数学模型（逻辑结构）以及定义在此数学模型上的一组操作

抽象数据类型可用（D，S，P）三元组表示
- D是数据对象；
- S是D上的关系集；
- P是对D的基本操作集。
定义抽象数据类型格式
1
2
3
4
5
ADT 抽象数据类型名{
数据对象<数据对象的定义>
数据关系<数据关系的定义>
基本操作<基本操作的定义>
}ADT 抽象数据类型名
- 数据对象、数据关系的定义用伪代码描述
- 基本操作定义格式为：
  - 基本操作名（参数表）
    - 赋值参数
      1
      s=area(r)
    - 引用参数
      1
      s=area(&s)
  - 初始条件（初始条件描述）
  - 操作结果（操作结构描述）——返回值

举例：

ADT  抽象数据类型名{
	Data
        数据对象的定义
        数据元素之间逻辑关系的定义
    Operation
        操作1
        	初始条件
        	操作结果描述
        操作2
        	......
        操作n
        	......
}ADT  抽象数据类型名

ADT  Circle{
	数据对象：D={r,x,y|r,x,y均为实数}
    数据关系：R={<r,x,y>|r是半径,<x,y>是圆心坐标}
    基本操作：
    Circle(&C,r,x,y)
        操作结果：构造一个圆
    double Area(c)
        初始条件：圆已存在
        操作结果：计算面积
    double Circumference(C)
        初始条件：圆已存在
		操作结果：计算周长
        ......
}ADT  Circle

算法

算法：对特定问题求解方法和步骤的一种描述，它是指令的有限序列

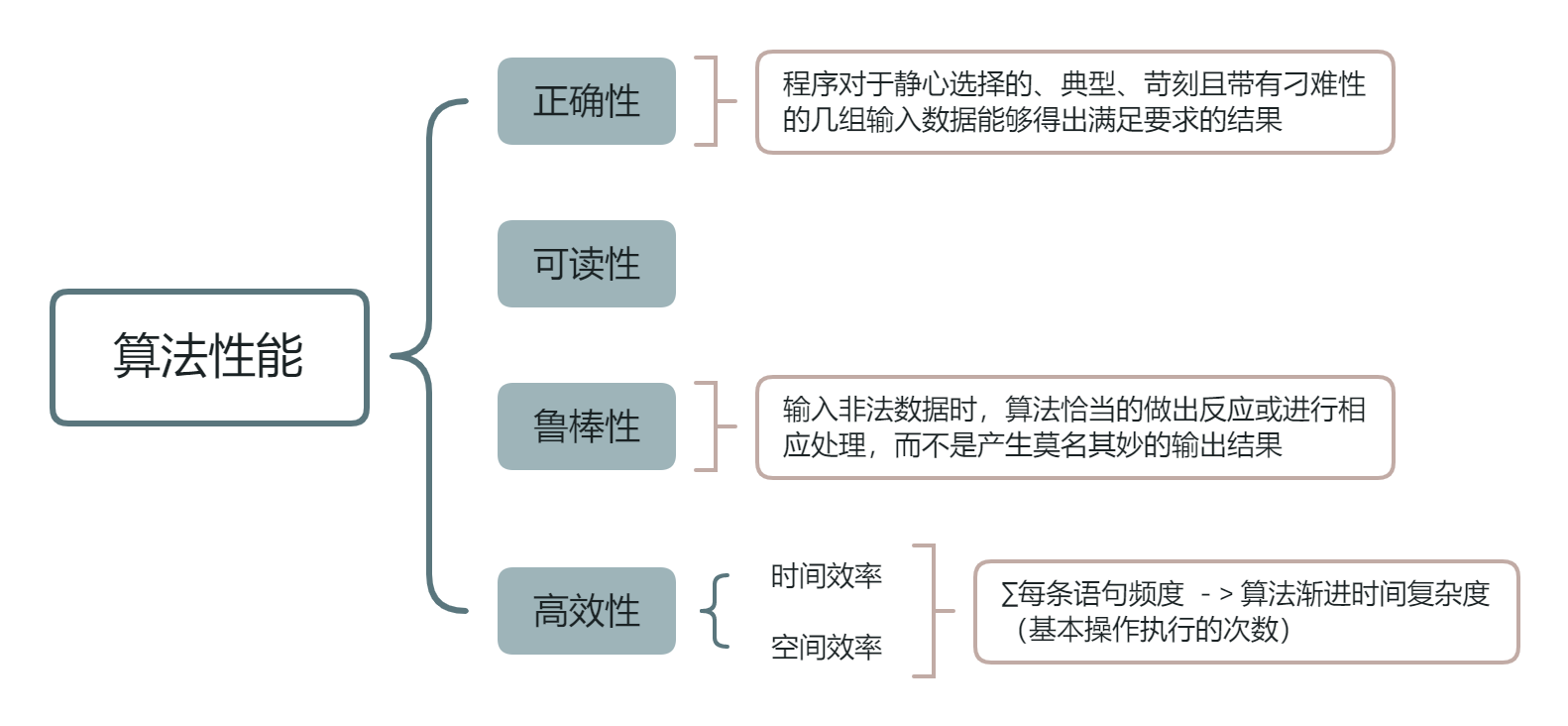
时间复杂度

时间复杂度可能与输入的数据有关，因此需要从最坏、最优、平均三个角度考察时间复杂度

举例1

# 例1：N×N矩阵相乘
for(i=1;i<=n;i++)		# n+1 -> 不成立也计入了判断次数
    for(j=1;j<=n;j++){	# n(n+1) -> 判断j<=n的次数n+1,外层循环执行n次判断
        c[i][j]=0;		# n*n -> 内外部循环均执行n次
        for(k=1;k<=n;k++)	# n*n*(n+1)
            c[i][j]=c[i][j]+a[i][k]*b[k][j];	# n*n*n
}

\[ 语句频度=T(n)=\sum_{i=1}^n\sum_{j=1}^n\sum_{k=1}^n1=\sum_{i=1}^n\sum_{j=1}^nn=\sum_{i=1}^nn^2=n^3=O(n^3) \]

举例2
1
2
3
4
5
# 例2：
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
for(k=1;k<=j;k++)
X=X+1;
\[ 语句频度=T(n)=\sum_{i=1}^n\sum_{j=1}^i\sum_{k=1}^j1=\sum_{i=1}^n\sum_{j=1}^ij=\sum_{i=1}^n\frac{i(i+1)}{2} \]
举例3
1
2
3
4
# 例3：
i=1;
while(i<=n)
i=i*2;
\[ 若循环执行1次：i=1*2=2\\ 若循环执行2次：i=2*2=2^2\\ 若循环执行3次：i=2*2=2^3,\\ 若循环执付x次：i=2^x\\ 设语句i=i*2执行次数为x次，由循环条件\\ i<=n\Longrightarrow 2^x<=n\Longrightarrow x<=log2n \]
总结：
- 时间复杂度的关键是找基本语句执行的次数
- 配合级数求解

空间复杂度

算法所需存储空间的度量，记作S(n)=O(f(n))，其中n为问题的规模
- 算法要占据的空间
  - 算法本身要占据的空间，输入/输出，指令，常数变量等
  - 算法要使用的辅助空间
- 举例1
  1
  2
  3
  4
  5
  # 【算法1】
  for(i=0;i<n/2;i++){
  t=a[i];
  a[i]=a[n-i-1];
  a[n-i-1]=t;
  \[ S(n)=O(1)原地工作 \]
- 举例2
  1
  2
  3
  4
  5
  # 【算法2】
  for(i=0;i<n;i++)
  b[i]=a[n-i-1];
  for(i=0;i<n;i++)
  a[i]=b[i];
  \[ S(n)=O(n) \]

第一章 绪论